Why the Martingale Strategy Fails in Casino Games

Why the Martingale strategy fails is a common question among casino players exploring betting systems. This article explains how probability, house edge, table limits, and psychological pressure prevent Martingale from working in real casino environments. By understanding the mathematics behind the system, players can approach casino games with realistic expectations and clearer perspective.

What the Martingale Strategy Claims to Do

Before examining why the Martingale strategy fails, it is important to understand the promise that makes it attractive to many casino players. At its core, the Martingale system suggests that losses can always be recovered by increasing the next wager until a win occurs.

This idea feels reassuring because it presents gambling as a problem that can be solved with persistence rather than probability. The simplicity of the concept creates a sense of control, leading players to believe that eventual success is inevitable.

The Illusion of Guaranteed Recovery

The Martingale strategy relies on the belief that one win can erase all previous losses. While this appears logical in theory, it assumes that wins will arrive before losses escalate beyond practical limits. In real casino environments, this assumption does not hold.

Losses can occur consecutively without warning, and the system offers no mechanism to reduce risk when those streaks appear.

Why Simplicity Creates False Confidence

Simple systems are psychologically appealing. The Martingale strategy removes complexity and replaces it with repetition, which can feel safer than navigating uncertainty. However, ease of understanding does not equate to effectiveness, especially in games governed by probability.

Probability Does Not Change After Losses

Casino games operate under fixed probability structures. These probabilities remain constant regardless of previous outcomes, bet size, or betting patterns.

Independent Events in Casino Games

Each spin, roll, or deal in a casino game is an independent event. This means that the outcome of one round has no influence on the next. A losing streak does not make a win more likely, just as a winning streak does not reduce the chance of another win.

The Martingale strategy assumes that probability will eventually favor the player, but independence ensures that outcomes remain unaffected by past results.

Why Losing Streaks Do Not Increase Winning Chances

Losing streaks are a normal feature of random systems. While they may feel unusual, they do not signal that probability is shifting. Expecting a win simply because losses have occurred misunderstands how randomness works in casino games.

The Mathematical Problem With Progressive Betting

Progressive betting systems like Martingale are built on mathematical assumptions that break down under real-world conditions.

Exponential Growth vs Linear Payouts

In most casino games, payouts increase linearly, while bet sizes in progressive systems grow exponentially. This imbalance creates a situation where risk increases much faster than potential reward.

As losses accumulate, wager sizes expand rapidly, exposing players to significant downside long before any theoretical recovery can occur.

Finite Bankrolls in Real-World Play

The Martingale strategy assumes access to unlimited funds. In reality, all players operate with finite bankrolls. Even substantial budgets can be exhausted quickly when bet sizes escalate during extended losing streaks.

Once a bankroll limit is reached, the recovery mechanism fails entirely, leaving losses unrecovered.

Table Limits Are Designed to Stop Martingale

Casino table limits are not arbitrary. They exist to protect the casino from excessive exposure and to maintain structured gameplay.

Why Unlimited Betting Is a Theoretical Concept

For Martingale to function as intended, players would need the ability to double bets indefinitely. This condition does not exist in real casinos, whether online or live. Maximum bet limits cap progression long before recovery is possible.

How Table Limits Break Recovery Cycles

When a table limit is reached during a losing sequence, the system collapses. At that point, the strategy can no longer proceed, and accumulated losses remain intact. This structural limitation alone is enough to invalidate Martingale as a reliable approach.

Psychological Pressure Created by Martingale

Beyond mathematical flaws, the Martingale strategy introduces intense psychological pressure that can negatively affect decision-making.

Escalating Bets and Emotional Stress

As bet sizes increase, so does emotional strain. Players may experience anxiety, urgency, and fear, especially when large wagers are required to continue the system. These emotional responses often lead to poor judgment and impulsive decisions.

Decision-Making Under Loss Pressure

Under stress, players are more likely to abandon limits, chase losses, or continue playing longer than intended. The Martingale strategy amplifies these risks by tying recovery directly to continued escalation.

Why Casinos Allow the Martingale Strategy

If the Martingale strategy were capable of producing consistent profits, casinos would not permit it. The reason it remains allowed is simple: it does not alter the mathematical advantage of the house.

House Edge Remains Unaffected

House edge is built into the rules of each casino game. No betting pattern can change this underlying structure. The Martingale strategy may rearrange the timing of wins and losses, but it does not influence expected value.

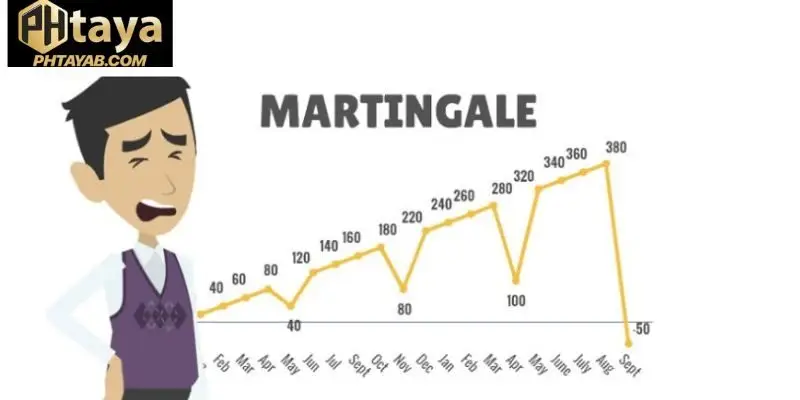
Short-Term Wins vs Long-Term Outcomes

Short-term success can and does occur with Martingale, which reinforces belief in the system. Over time, however, probability reasserts itself. Extended play exposes the system’s vulnerability to loss escalation and structural limits.

Conclusion

The Martingale strategy fails because it conflicts with the mathematical structure of casino games, where probability, bankroll limits, and table rules define outcomes. Understanding these limits helps players approach casino play with realistic expectations, a perspective reflected in the approach supported by Ph taya